백준 9020, 골드바흐의 추측(자바/java)
백준 9020, 골드바흐의 추측(자바/java)
문제
1보다 큰 자연수 중에서 1과 자기 자신을 제외한 약수가 없는 자연수를 소수라고 한다. 예를 들어, 5는 1과 5를 제외한 약수가 없기 때문에 소수이다. 하지만, 6은 6 = 2 × 3 이기 때문에 소수가 아니다.
골드바흐의 추측은 유명한 정수론의 미해결 문제로, 2보다 큰 모든 짝수는 두 소수의 합으로 나타낼 수 있다는 것이다. 이러한 수를 골드바흐 수라고 한다. 또, 짝수를 두 소수의 합으로 나타내는 표현을 그 수의 골드바흐 파티션이라고 한다. 예를 들면, 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, 10 = 5 + 5, 12 = 5 + 7, 14 = 3 + 11, 14 = 7 + 7이다. 10000보다 작거나 같은 모든 짝수 n에 대한 골드바흐 파티션은 존재한다.
2보다 큰 짝수 n이 주어졌을 때, n의 골드바흐 파티션을 출력하는 프로그램을 작성하시오. 만약 가능한 n의 골드바흐 파티션이 여러 가지인 경우에는 두 소수의 차이가 가장 작은 것을 출력한다.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고 짝수 n이 주어진다.
출력
각 테스트 케이스에 대해서 주어진 n의 골드바흐 파티션을 출력한다. 출력하는 소수는 작은 것부터 먼저 출력하며, 공백으로 구분한다.
[풀이]
(1)
문제에서 나와있는대로 0 ~ 10000 까지의 배열을 생성하고
에라토스테네스의 체를 이용하여 소수 구하기.
public class Test {
0부터 10000까지의 소수를 판별할 배열 생성.
public static boolean[] prime = new boolean[10001];
public static void main(String[] args) {
getPrime();
소수 구하는 알고리즘:
static void getPrime() {
prime[0] = prime[1] = true;
for (int i = 2; i <= Math.sqrt(prime.length); i++) {
if (prime[i]) continue;
for (int j = i * i; j < prime.length; j += i) {
prime[j] = true;
}
}
}
}
(2)
테스트 케이스(TestCase)를 입력받아 반복문을 만들고 짝수 n 을 입력받기.
먼저 테스트케이스 TestCase를 입력받아
while 반복문 안에서 n을 입력받는다.
import java.util.Scanner;
public class Test {
public static boolean[] prime = new boolean[10001];
public static void main(String[] args) {
getPrime();
int TestCase = in.nextInt();
while (TestCase-- > 0) {
int n = in.nextInt();
}
}
소수 구하는 알고리즘.
static void getPrime() {
prime[0] = prime[1] = true;
for (int i = 2; i <= Math.sqrt(prime.length); i++) {
if (prime[i]) continue;
for (int j = i * i; j < prime.length; j += i) {
prime[j] = true;
}
}
}
}* while( variable -->0)
variable--; variable > 0; 이 두 가지를 합쳐놓은 것.
0 보다 조건 값을 뺀 값이 클 경우,
-- (증감 연산자)와 > (꺾쇠괄호)를 합쳐 놓은 형태임.
(3)
짝수 n 에 대하여 두 소수 구하기
여기서 중요한 포인트. 만약 정답이 여러개일 경우 두 소수의 차가 작은 것을 출력하기.
예를들어 10을 생각해보자. 두 소수의 합이 10인 소수는 다음과 같다.
3+7 = 10
5+5 = 10
여기서 두 소수의 차가 작은 5, 5를 찾아야 한다.
어떤 수든 그 수의 반절(10이면 5+5, 18이면 9+9)로 나눴을 때
두 수의 차가 가장 적기 때문에
절반으로 나눈 수부터 찾는 것이 효과적일 것이다.
예시로 입력받은 짝수 n이 16일 경우..
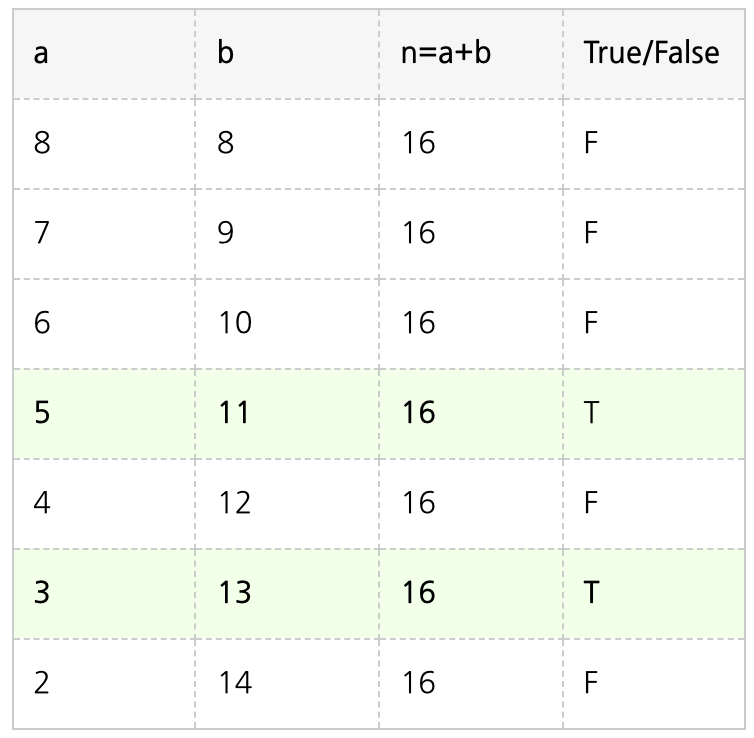
a와 b가 소수가 아니라면
a는 1 감소, b는 1 증가시키면서
a와 b가 소수일 때 까지 찾는 것이다.
이렇게 8,8부터 찾다가 5, 11일 때 즉 두 수가 모두 소수일 때
반복문을 종료하고 해당 수를 출력하면 되겠다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static boolean[] prime = new boolean[10001];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
getPrime();
int TestCase = Integer.parseInt(br.readLine());
while (TestCase-- > 0) {
int n = Integer.parseInt(br.readLine());
int firstPartition = n / 2;
int secondPartition = n / 2;
while (true) {
if (!prime[firstPartition] && !prime[secondPartition]) {
System.out.println(firstPartition + " " + secondPartition);
break;
}
firstPartition--;
secondPartition++;
}
}
}
static void getPrime() {
prime[0] = prime[1] = true;
for (int i = 2; i <= Math.sqrt(prime.length); i++) {
if (prime[i]) continue;
for (int j = i * i; j < prime.length; j += i) {
prime[j] = true;
}
}
}
}
여기서 한단계 더 ! 가자면
출력할 케이스들이 많을 때
StringBuilder 로 출력할 문자열을 하나로 묶어서
마지막에 한 번에 출력하면 더 좋다.
(이 방법은 구글링 하다가 여기서 알게 됐다..👍🏻 )
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Test {
public static boolean[] prime = new boolean[10001];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
getPrime();
int T = Integer.parseInt(br.readLine());
while (T-- > 0) {
int n = Integer.parseInt(br.readLine());
int firstPartition = n / 2;
int secondPartition = n / 2;
while (true) {
if (!prime[firstPartition] && !prime[secondPartition]) {
sb.append(firstPartition).append(' ').append(secondPartition).append('\n');
break;
}
firstPartition--;
secondPartition++;
}
}
System.out.print(sb);
}
static void getPrime() {
prime[0] = prime[1] = true;
for (int i = 2; i <= Math.sqrt(prime.length); i++) {
if (prime[i]) continue;
for (int j = i * i; j < prime.length; j += i) {
prime[j] = true;
}
}
}
}한단계에 이만큼 서능 차이가 난다!
특히 가장 처음 제출했던 건 Scanner 사용한 것인데 BufferedReader와 확연한 차이..