고정 소수점과 부동소수점 (컴퓨터에서의 실수 표현)
실수의 표현 방식 💡
컴퓨터에서 실수를 표현하는 방법은 정수에 비해 훨씬 복잡하다.
왜냐하면, 컴퓨터에서는 실수를 정수와 마찬가지로 2진수로만 표현해야 하기 때문.
따라서 실수를 표현하기 위한 다양한 방법들이 연구되었으며, 현재에는 다음과 같은 방식이 사용되고 있다.
1. 고정 소수점(fixed point) 방식
2. 부동 소수점(floating point) 방식
1. 고정 소수점 방식
실수는 보통 정수부와 소수부로 나눌 수 있다.
따라서 실수를 표현하는 가장 간단한 방식은 소수부의 자릿수를 미리 정하여,
고정된 자릿수의 소수를 표현 하는 것.
32비트 실수를 고정 소수점 방식으로 표현하면 다음과 같다.
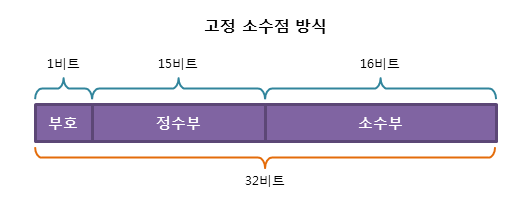
앞의 16비트는 부호와 정수부를,
뒤의 16비트는 소수부를!
16비트로 예를 들어보자.
앞의 8비트는 정수 부분을, 나머지 8비트는 소수 부분을 위해서 할당하면 될 것이다.
예를 들어 5.34(10)의 경우에는 101.010101110...(2)의 무한 소수 형태의 이진수가 되는데,
앞서 말한 방식으로는 16비트의 다음 숫자가 된다.
00000101 01010111(2)
이런 표기 방법은 앞선 포스팅들에서 다뤘던 정수 표현 방법을 정수 부분과 소수 부분에 각각 적용한 것.
아주 큰 숫자가 아니거나 소수점 아래가 아주 길어서 정확한 실수 값을 사용하지 않는 경우라면 사용할 수 있다.
즉, 소수점의 위치를 고정시켜 표현하는 방식인데 크고 정밀한 실수를 표현하지 못하기 때문에,
컴퓨터에서는 사용되지 않는다.
일반적으로 컴퓨터에서는 정수 표현에 초과 표기법(excess notation)을,
소수 표현에 부동 소수점 표기법(floating-point notation)을 사용한다.
요점 : 고-소 방식은 정수부와 소수부의 자릿수가 크지 않으므로, 표현할 수 있는 범위가 매우 적다는 단점이 있다.
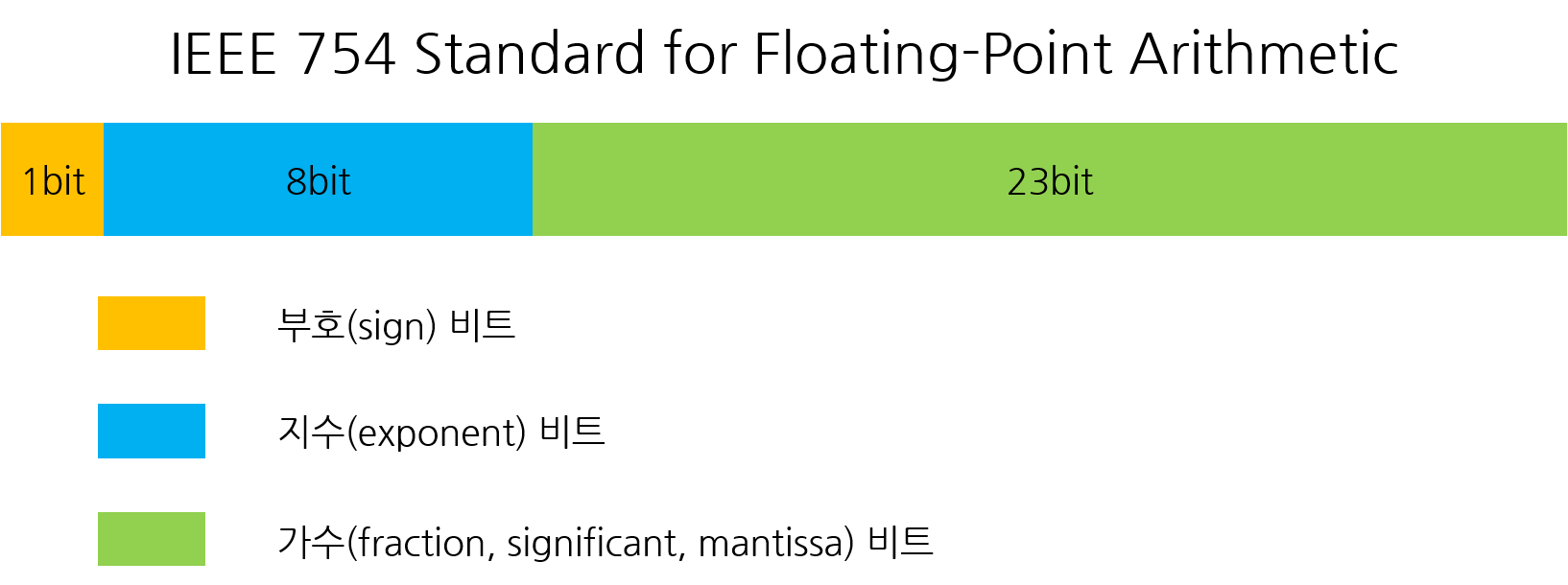
2. 부동 소수점 (floating point) 방식
실수는 보통 정수부와 소수부로 나누지만, 가수부와 지수부로 나누어 표현할 수도 있다.
부동 소수점 방식은 이렇게 하나의 실수를 가수부와 지수부로 나누어 표현하는 방식~!
앞서 살펴본 고정 소수점 방식은 제한된 자릿수로 인해 표현할 수 있는 범위가 매우 작았는데,
부동 소수점 방식은 매우 큰 실수까지도 표현할 수 있다.
아까의 0.34를 다시 예시로 들어보자.
# Ex.1
(1) 부동소수점 바꾸기, 첫번째 단계 이진법 변환
0.34(10)를 컴퓨터에서 사용하기 위해 이를 이진수로 바꾸면 다음처럼 무한 소수가 된다.
0.010101110...(2)
(2) 정규형으로 바꾸기, 두번째 단계
이를 정규형(nomalized form)으로 바꿔보자.
정규형이란 정수 부분에 한자리수 1만 남기는 것을 말한다.
정수를 한 자리수만 남김으로써 실수의 표현법을 통일하려는 의도로 사용되는데,
정규형을 사용하지 않으면 10.10*2^(-3)이나 0.1010*2^(-1) 등 하나의 숫자에 대해 너무나 많은 표현이 가능하기 때문이다. 아무튼 위 숫자에 대한 정규형은 아래와 같다.
1.0101110...*2^(-2)
(3) 지수부 #초과표현 하기, 세번째 단계
이 숫자에서 지수와 가수를 나누어 아래 형식처럼 표현한다. 8비트를 가정했을 때, 각 부분에 다음처럼 비트를 할당한다고 생각해보자.

여기서 지수(exponent)를 위해 3비트를 할당했기 때문에 #초과표현 (excess 3 representation: 3초과표현)을 사용한다.
즉, 정규형으로 표현된 1.0101110*2^(-2)를 표현하기 위해서는 지수가 -2이기 때문에
3을 초과시켜서 1을 적음! (-2+3=1).
그런데 왜?
왜 초과표현을 사용하는걸까?
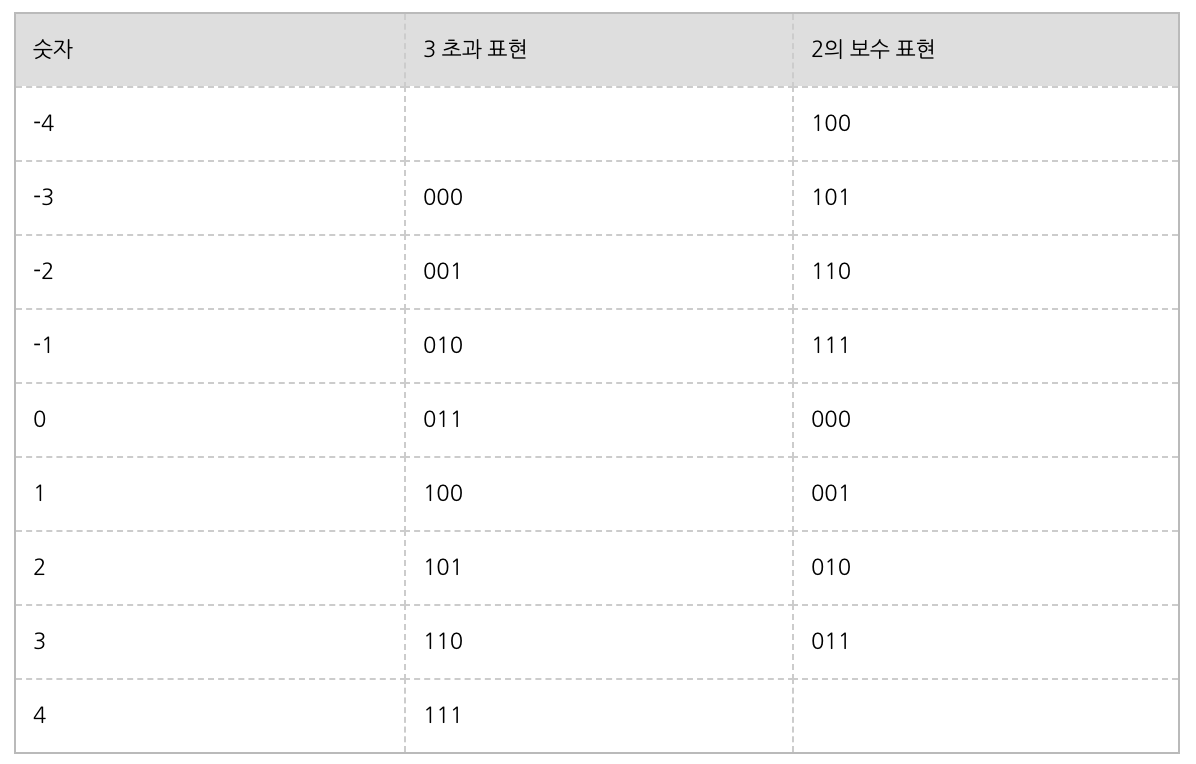
#초과표현
초과 표현에 대해 좀 더 알아보자.
초과 표현은, N bit에서 2^(N-1)-1 을 초과시켜 표현하는 것이다.
아래의 표는 3초과 표현 이다.
아래의 두 수는 정규형으로 표현된 수이다.
1.000 * 2^0
1.111 * 2^(-1)
두 숫자 중 어떤 수가 큰 수인지 어떻게 알 수 있을까?
이를 비교하려면 10진수로 변환하여 비교하거나 지수 값을 동일하게 바꾸면 된다.
두 번째 수의 지수를 첫 번째와 동일하게 바꿔보자!
1.000 * 2^0
0.1111 * 2^0
하지만 정규형에서는 이런 과정을 거칠 필요없이(가수를 볼 필요 없이) 지수가 큰 수가 큰 수이다.
왜냐믄 정규형에서는 두 수의 부호가 같은 경우는 가수가 아무리 커도 지수가 큰 수가 큰 수이기 때문..
지수 값이 차이가 난다면 가수를 볼 필요가 없고, 지수 값이 같다면 가수를 비교해야 한다.
위의 예를 다시 표현하면,
0 011 1000 (1.000*2^0)
0 010 1111 (1.111*2^(-1))
이렇게 지수와 가수의 상대적인 위치 배치와 지수에 대한 초과 표기법을 사용하기 때문에 실수의 대소 비교 연산을 수행할 때는, 따로 실수라고 생각하지 않고 정수의 대소 관계처럼 생각해도 좋다.
이처럼 지수 영역을 위해서 초과 표현을 사용하면 같은 부호일 경우에는 전체의 비트 패턴을 정수처럼 생각해서 대소 관계를 파악할 수 있게 된다. 실수의 연산보다 정수의 연산이 더 빠르기 때문에 이는 큰 장점.
이는 초과 표현의 중요한 특징 중 하나다.
이어서 예시를 마저 끝내자.
가수는 1.0101110이기 때문에 0101110이 되는데,
가수부분으로 4비트를 할당했기 때문에 0101이 된다. *앞의 정수부분 1은, 모든 정규화 수가 1.-으로 시작하니까, Hidden Bit라 하며 정규화 할때 무시하고 쓴다. 따라서 이를 그대로 표현하면-
부호 지수 가수
0 001 0101
지수 표현을 위한 비트수와 가수 표현을 위한 비트수의 할당에 따라 표현할 수 있는 숫자의 범위와 정확도가 결정된다. 즉, 지수에 더 많은 비트를 할당하면 더 큰 절대값을 가지는 숫자의 표현이 가능해지고, 가수에 더 많은 비트를 할당하면 보다 정확한 수를 표현할 수 있게 된다.
다시말해 0.34(10)는, 8비트 컴퓨터 내부에서는 0001 1010(2)라는 이진수로 저장되고,
이를 다시 정규형으로 표현하면 1.010*2^(-2)가 되고,
이 숫자는 십진수 0.3125이다.
원래 표현하려던 숫자와 오차가 발생한다.
# 예시 2
이번에는~ 고정 소수점으로 나타낸 263.3을 16비트의 부동 소수점 방식으로 변환해 보자.
고정소수점으로는 100000111.010011001100110... 으로 표현되던 것을,
1. 정규화
맨 앞에 있는 1 바로 뒤로 소수점을 옮겨서 표현하도록 변환한다.
그러면 1.00000111010011001100110... * 2^8.
2^8의 8이 지수.
2.지수부
#바이어스 (윌 바이어스..?!크크)
일단 여기서 지수부는 8bit를 쓸 수 있으니까,
8bit의 표현가능 숫자의 범위는 -128부터 127.
그리고 여기엔
부호부가 존재치 않기 때문에 0000 0000을 -127로, 1111 1111을 128로 정의하기로 약속.
그래서 0이라는 값이 부호없는 수로하면
127 + 지수를 기록함. 그러니까 127 + 8 인 것.)
그럼 이 방식에 따라서,
부호 비트(1 bit) : 0 (양수)
지수 비트(8 bit) : 10000111 (127 + 8 = 135)
가수 비트(23 bit) : 00000111010011001100110
하지만!
여기서도 0.010011001100110은 정확히 0.3을 나타낼 수는 없다.
이를 다시 10진수로 나타내 보면 0.29998779296875이라는 값이 나온다..
아까와 마찬가지로 원래 표현하려던 숫자와 오차가 발생.
여기서의 중요한 결론 :
부동소수점의 특징 💡
1. 지수부 : 크기 비교를 빠르게 할 수 있다. (고정소수점에 비해선 연산속도가 느리다.)
2. 부동 소수점은 0 과 0.01을 표현하지 못하는 등 오차가 있다.
실수를 '정확히 표현'하지 못하는 문제! (고정소수점에 비해선 작은 값을 표현할 수 있지만)
3. 지수와 가수의 상대적인 위치 배치의 문제로, 초과표현을 사용.(지수부 뺄셈 후 연산을 해야함)
#Hidden Bit
아까 한번 언급하긴 했는데, 정규화를 하면 정수부분은 항상 1이 된다.
ex. 1.0101110...*2^(-2)
그렇담 2진수 정규형으로 표현된 수의 정수 부분은 항상 1이니까, 표현하지 않아도 되는거 아닐까?
그래서 1을 숨기로 하고, 이를 히든비트라 부르기로 한다. 이를 사용하면 가수부의 1비트를 더 사용할 수 있다!
ex. 1.0101110...*2^(-2)
여기서, 히든비트를 사용하지 않으면 0 001 1010
사용한다면, 0 001 0101
이러면 원래 1.010*2^(-2)까지만 표현이 가능했던 비트가 1.0101*2^(-2)까지 표현할 수 있게됨으로써
더 정확한 숫자를 표현할 수 있다!
#0을 표현하는 방법 : Special Values
위의 히든비트를 사용하면,
3초과 표현을 사용했을때 0 000 000(2)는 1.0000*2^(-3)가 되어 0.125가 된다.
즉 0이 되지 못한다는 것인데, 이를 위해 0 000 0000(2)를 그냥 0으로 사용하자는 약속을 한다.
이것이 십진수 진짜 0을 위한, Special Values의 개념이다.

이를 정리하면,
8비트 부동소수점 표기법에서는 아래의 범위 만을 커버할 수 있다.

위 표의 양 끝은, 우리가 표현할 수 있는 수의 범위를 넘어서서, #overflow 가 발생하는 범위이고,
주황색으로 표시된 부분은 우리가 표현한 0과 1 사이의 더 촘촘한 간격의 수,
그 앞은 0과 1 사이의 수, 즉 오버플로우의 반대인 #Underflow 가 발생하는 범위이다.
지금까지 우리는 정규화를 통해 이진수로 실수를 표현했는데,
이때 가장 앞의 1을 제외하고 bit값을 채워넣어 표현했다.
다시 말하자면 정규화해 표현된 모든 수는 숨겨진 히든비트로 인해 가수부가 항상 1.~인 수 만을 표현할수 있었던 것.
1.00 * 2^-126 보다 작은 0.11 * 2^-126의 경우 지수부의 표현범위를 벗어나므로 표현할 수 없었다.
그래서,
# Denormalized : 비정규화
이러한 Special value 의 경우, 비정규화된 수를 도입하여 해결한다.
비정규화된 수를 표현하는 방법은 다음과 같다.
- 지수부(e)의 모든 bit는 0으로 채우고,
-부호부(s)와 가수부(소수부)의 값을 표현한다.

모든 비트가 0인 경우는 0을 나타내고,
지수부의 비트가 0이지만 가수부의 비트가 0이 아닐경우,
유효수에서 정수값을 1이 아닌 0으로 한다.
그리고 지수값을 -126으로 하자 약속한다.
예를들어 정규화 계산 결과로 나온 값이 1.010111 x 2^-129 이라고 하자.
그런데 -129는 지수가 표현할 수 있는 범위를 벗어나므로
0.001010111 x 2^-146으로 표기해야 한다.
그치만 유효숫자는 최상위 비트를 1로 가정하고 생략하여 저장하고 있어서
지수부에 동일하게 -126을 사용할수 없다.
만약 그렇게 한다면 1.001010111과 0.001010111을 구분할 수 없다!
따라서 이 경우렌 지수부에 0을 저장하여 정상적인 경우와 구분한다.
그리고 표현할수 있는 범위를 넘는 큰 수는 지수부 모든 칸을 1로 채우고, 가수부는 모두 0으로 채워
무한대로 인식하고,
너무 작아서 표현할 수 없는 수는 지수부 모든칸을 1로 채우고, 가수부는 0으로 채우지 않아
Not a number 로 인식한다.
'컴퓨터 시스템' 카테고리의 다른 글
| 백준 1476, 날짜계산 (자바/java) (0) | 2022.04.11 |
|---|---|
| 백준 2309, 일곱 난쟁이 (자바/java) (1) | 2022.04.11 |
| 컴퓨터에서의 정수표현 (부호있는 정수, 2의 보수) (1) | 2021.07.20 |
| 가상메모리, 페이징, 세그멘테이션, 페이지교체 알고리즘 (0) | 2021.07.20 |
| 메모리 Memory (0) | 2021.07.20 |





댓글